Cassandra Goal-Seeking Model
A new tool in the Cassandra toolbox to tune and optimise Infrastructure Deterioration Models
In my previous post, I discussed the concept of an Asymmetric Loss Function and how it can be used as a metric for comparing how well different models do to meet your network Key Performance Indicators (KPIs) under a given budget constraint.
The Asymmetric Loss Function can also be used as a way to get the model to chase after a specific objective such as maintaining the network to ensure that a certain level of structural distress is not exceeded. In this approach, we specify a KPI such as “% of Network Length with Pavement Distress Index exceeding 10” and then use this to represent our goal.
Let’s assume the network’s current value for this KPI is 8%. That is, currently, 8% of the network length has a Pavement Distress Index (PDI) exceeding 10. Let’s further assume that we are looking for the budget levels that will maintain this KPI at its current level of 8% (we can specify any target level, but for this example I will assume the initial value of 8% is our target).
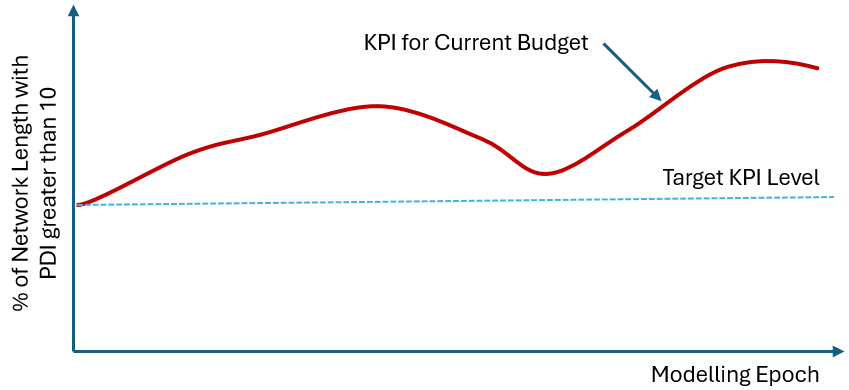
When we run the model with our current planned budget, we may get an Asymmetric Loss Function for our KPI that looks like this:
In this scenario, the asymmetric loss is the area between the target KPI level and the red line which represents the output from our model when we use the current budget level. Clearly, the current budget is not sufficient to meet our KPI. But how do we find the budget level that will satisfy the KPI criterion?
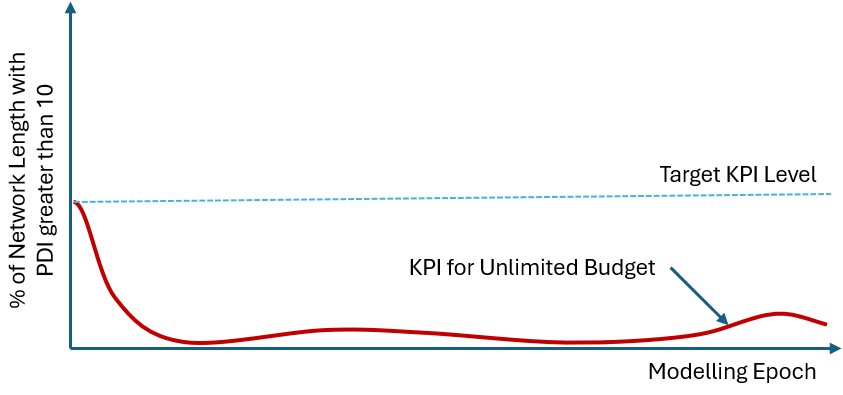
One approach often used to answer the question “what does the network need?” is to provide a heavily inflated budget and use the spending from that model to guide our budget constraints. However, this is unlikely to work because (a) the model will (unrealistically) use the inflated budget to address the entire backlog in the first few years; and (b) thereafter, the model may keep the network in an unrealistic pristine condition.
Such a situation is shown in the figure below. Clearly using an heavily inflated (or “unlimited”) budget will not provide us with the information we are looking for:
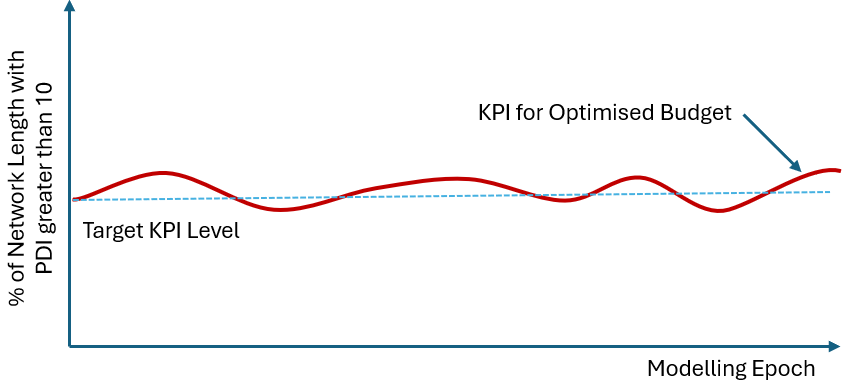
The new Goal-Seek function in Cassandra addresses this problem by allowing the modeller to target a specific KPI level over the modelling period. With this tool, we can specify search ranges for each budget category and each period group (e.g. period 1 to 10, 11 to 20, etc). The Cassandra Goal-Seek model will then use Latin Hypercube Sampling to create a search grid that varies the budgets for each category in the specified period ranges.
The model will then run for each of these variations and report the Asymmetric Loss value for each variation. If you run this over enough variations, you will find a budget scenario that will keep your KPI as close as possible to the target KPI level:
As can be expected, such a goal-seeking run can take quite some time to complete. Fortunately Cassandra was built with performance in mind, and the goal seeking process allows models to be run in parallel, so that all of the available cores of your computer can work on different budget variations concurrently.
In a recent study, we ran 2,000 budget variations for a moderately sized network of about 2,600 elements. The model we used was a Multi-Criteria Decision Analysis (MCDA) model which ran over a 30-year analysis period. On my moderately powerful desktop computer, Cassandra completed the goal-seek process involving 2,000 model runs in a under two hours.
Of course, if you are modelling a larger network or using the Benefit-Cost Analysis (BCA) model type, the run time will be considerably longer. But even in these scenarios, running the model overnight should be sufficient to help you find your optimal budget splits over different modelling periods.
The goal-seek model can also be used to optimise some of the thresholds used in your model. Currently, the Cassandra Goal-Seek model allows you to specify and investigate variations for three types of model variables:
Budget levels for different categories over different periods;
Lookup values such as thresholds and calibration factors;
Weight functions for the different MCDA objectives such as cost, treatment suitability etc.
The use of the Goal-Seek model to optimise some of the arbitrarily selected thresholds and calibration factors can be particularly useful. In this approach, you can set a strict and fixed budget constraint and then run a Goal-Seek model to find the values for your thresholds that will get your KPI as close as possible to the target value. This is, in effect, a form of optimisation, since you are finding the values of your threshold factors that will optimise adherence to your KPI over the modelling period.
We have recently used the Goal-Seeking model in a real-world analysis and found that the Goal-Seek model not only saved hours of time but also allowed us to gain confidence in setting values for certain thresholds that would otherwise have been set rather arbitrarily based only on domain experience.
That’s is for this post!
Please help us grow the audience for our newsletter by sharing this post with colleagues and friends that may be interested in this topic.